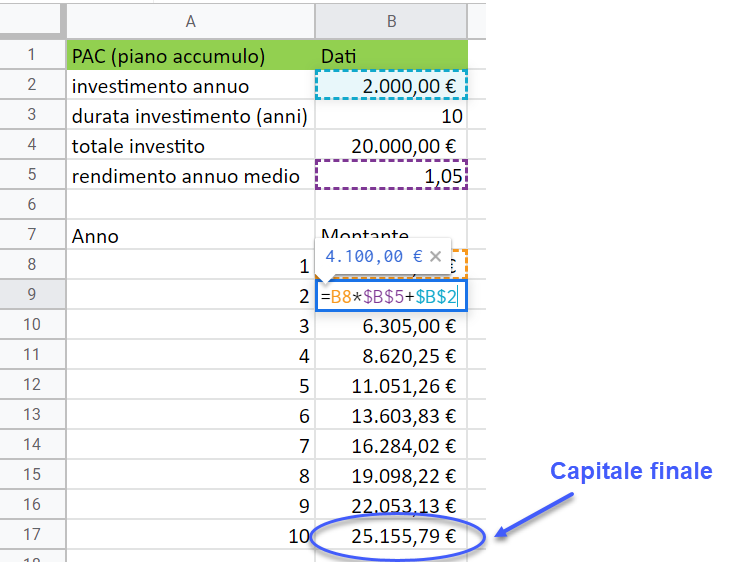
✅ L’interesse composto si calcola così: Capitale × (1 + Tasso)^Anni. Esempio: 1000€ al 5% per 3 anni diventano 1157,63€, crescita esponenziale!
L’interesse composto si calcola applicando l’interesse non solo al capitale iniziale, ma anche agli interessi maturati nei periodi precedenti. La formula generale per calcolare l’importo finale con interesse composto è:
A = P (1 + r/n)^(nt)
- A è l’importo finale (capitale + interessi)
- P è il capitale iniziale
- r è il tasso di interesse annuale in decimale
- n è il numero di capitalizzazioni dell’interesse per anno
- t è il numero di anni
Ad esempio, se investi 1.000 euro ad un tasso annuo del 5% con capitalizzazione annuale per 3 anni, il calcolo sarà:
A = 1000 × (1 + 0.05/1)^(1×3) = 1000 × 1.157625 = 1.157,63 euro
Quindi, dopo 3 anni, il tuo capitale sarà cresciuto a 1.157,63 euro grazie all’interesse composto.
Approfondimento sull’Interesse Composto
L’interesse composto è un concetto fondamentale nella finanza che permette di far crescere un capitale in maniera esponenziale nel tempo. A differenza dell’interesse semplice, che calcola gli interessi solo sul capitale iniziale, l’interesse composto tiene conto di ogni interesse maturato, reinvestendolo automaticamente.
Questo meccanismo può aumentare significativamente il rendimento di un investimento o, nel caso di debiti, la somma da restituire. È importante conoscere la frequenza con cui gli interessi vengono capitalizzati (annuale, semestrale, trimestrale, mensile) poiché questo influisce direttamente sul risultato finale.
Di seguito analizzeremo:
- Le diverse frequenze di capitalizzazione e il loro impatto
- Come utilizzare la formula in contesti pratici diversi
- Esempi dettagliati con capitali, tassi e periodi differenti
- Consigli per calcolare interessi composti in modo semplice
Formula dell’Interesse Composto: spiegazione dettagliata dei parametri
Per capire a fondo come funziona l’interesse composto, è fondamentale partire dalla sua formula matematica, che permette di calcolare il valore futuro di un capitale investito o finanziato in base a un tasso di interesse che si accumula nel tempo. La formula generale è:
F = P (1 + r/n)^(nt)
Dove ciascun parametro rappresenta un elemento chiave:
- P (Principale) – È il capitale iniziale investito o prestato. Ad esempio, se investi 1.000 euro, P sarà 1.000.
- r (tasso di interesse annuale) – Indica il tasso percentuale di interesse annuo applicato. Se il tasso è del 5%, r sarà 0,05.
- n (frequenza di capitalizzazione) – Indica quante volte l’interesse viene composto nell’anno. Può assumere valori come 1 (annuale), 4 (trimestrale), 12 (mensile) o addirittura 365 (giornaliero).
- t (tempo) – È il periodo totale espresso in anni durante il quale il denaro resta investito o preso in prestito.
- F (valore futuro) – È il montante finale, ovvero la somma del capitale iniziale più gli interessi maturati in tutto il periodo considerato.
Perché la formula funziona così?
Ogni periodo di capitalizzazione, l’interesse maturato viene aggiunto al capitale, incrementando così la base su cui calcolare gli interessi successivi: è il classico esempio del “interessi sugli interessi”. Questo meccanismo crea un effetto esponenziale, che può portare il capitale a crescere notevolmente nel lungo termine.
Un esempio pratico
Immaginiamo di investire 2.000 euro a un tasso del 6% annuo, con capitalizzazione mensile (n = 12), per un periodo di 5 anni. Sostituendo nella formula:
- P = 2000
- r = 0.06
- n = 12
- t = 5
Calcoliamo:
F = 2000 × (1 + 0.06 / 12)^(12 × 5) = 2000 × (1 + 0.005)^(60)
Questo si traduce in:
F ≈ 2000 × 1.34885 = 2.697,70 euro
Così, dopo 5 anni, il capitale è cresciuto di circa 697,70 euro, grazie all’effetto degli interessi composti.
Consigli pratici
- Più alta è la frequenza di capitalizzazione (n), maggiori saranno gli interessi generati nel tempo: capitalizzare mensilmente o giornalmente fa una differenza significativa rispetto alla capitalizzazione annuale.
- Calcolare con precisione il parametro r è fondamentale: ricordati di usare la forma decimale (es. 5% = 0,05).
- Per investimenti a lungo termine, l’interesse composto svolge un ruolo centrale nella crescita del capitale. Pensare in ottica pluriennale può aumentare sensibilmente i guadagni.
Tabella di confronto: effetti della capitalizzazione
| Frequenza di Capitalizzazione (n) | Montante dopo 5 anni (€) | Interesse Totale (€) |
|---|---|---|
| Annuale (1) | 2.676,00 | 676,00 |
| Semestrale (2) | 2.685,06 | 685,06 |
| Trimestrale (4) | 2.690,41 | 690,41 |
| Mensile (12) | 2.697,70 | 697,70 |
| Giornaliera (365) | 2.699,58 | 699,58 |
Fonte dati: calcoli basati sulla formula dell’interesse composto.
In sintesi, conoscere i parametri della formula dell’interesse composto e il loro impatto permette di gestire al meglio i propri investimenti o prestiti, ottimizzando i rendimenti o i costi nel modo più consapevole possibile.
Domande frequenti
Che cos’è l’interesse composto?
L’interesse composto è l’interesse calcolato sia sul capitale iniziale che sugli interessi accumulati nei periodi precedenti.
Qual è la formula per calcolare l’interesse composto?
La formula è: A = P (1 + r/n)^(nt), dove A è l’importo finale, P il capitale iniziale, r il tasso di interesse annuo, n il numero di capitalizzazioni annuali e t il tempo in anni.
Come si applica l’interesse composto in un esempio pratico?
Se investi 1000€ a un tasso annuo del 5% con capitalizzazione annuale, dopo 3 anni l’importo sarà A = 1000 (1 + 0.05/1)^(1*3) = 1157,63€.
Quali sono i vantaggi dell’interesse composto?
L’interesse composto aumenta esponenzialmente il valore dell’investimento nel tempo, incentivando il risparmio a lungo termine.
Qual è la differenza tra interesse semplice e interesse composto?
L’interesse semplice si calcola solo sul capitale iniziale, mentre l’interesse composto include anche gli interessi accumulati.
| Parametro | Descrizione | Esempio |
|---|---|---|
| P | Capitale iniziale | 1000€ |
| r | Tasso di interesse annuo | 5% (0,05) |
| n | Numero di capitalizzazioni all’anno | 1 (annuale) |
| t | Durata in anni | 3 |
| A | Importo finale (capitale + interessi) | 1157,63€ |
Ti invitiamo a lasciare i tuoi commenti qui sotto e a esplorare altri articoli sul nostro sito che potrebbero interessarti.